



Next: 2.2.4 Variation of with
Up: 2.2 The Fundamental Plane
Previous: 2.2.2 Is the FP
2.2.3 The Physics Underlying the FP
To interpret the empirical FP relation,
we need to relate the observable quantities
to the physical quantities.
The observable quantities are
a radius
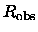 ,
a velocity
,
a velocity
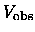 ,
and
a mean surface brightness
,
and
a mean surface brightness
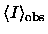 .
One particular choice of observables is
.
One particular choice of observables is
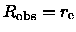 ,
,
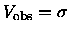 ,
and
,
and
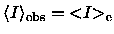 .
Other choices could be used,
for example
.
Other choices could be used,
for example
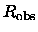 could be taken as the core radius in a King model fit.
The following considerations are inspired by
Djorgovski, de Carvalho, & Han (1988).
could be taken as the core radius in a King model fit.
The following considerations are inspired by
Djorgovski, de Carvalho, & Han (1988).
For a bound system, such as a galaxy,
the sum of the kinetic and potential energy must be less than zero.
This can be written as
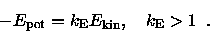 |
(2.10) |
For a virialized system
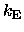 has the value 2.
We define
has the value 2.
We define
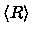 and
and
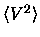 as the mean radius and mean square velocity
that enters the expressions for the potential and kinetic energy,
respectively, i.e.
as the mean radius and mean square velocity
that enters the expressions for the potential and kinetic energy,
respectively, i.e.
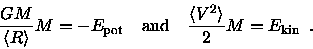 |
(2.11) |
We can now write the energy equation (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) ) as
) as
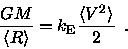 |
(2.12) |
We relate the observable quantities
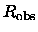 ,
,
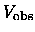 ,
and
,
and
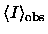 to the
physical quantities
to the
physical quantities
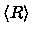 ,
,
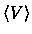 ,
and luminosity L through
,
and luminosity L through
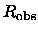 |
= |
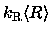 |
(2.13) |
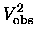 |
= |
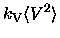 |
(2.14) |
| L |
= |
 |
(2.15) |
The parameters
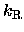 ,
,
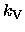 ,
and
,
and
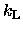 reflect the
density structure, kinematical structure, and luminosity structure
of the given galaxy.
Obviously, they depend on the choice of observables
(e.g. whether
the r1/4 half-light radius
reflect the
density structure, kinematical structure, and luminosity structure
of the given galaxy.
Obviously, they depend on the choice of observables
(e.g. whether
the r1/4 half-light radius
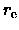 or
the King core radius
or
the King core radius 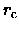 is used for
is used for
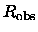 ).
From the energy equation (
).
From the energy equation (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) )
we can find the mass M as
)
we can find the mass M as
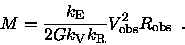 |
(2.16) |
We can now find a relation for
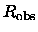 ,
and compare it with the the FP
,
and compare it with the the FP
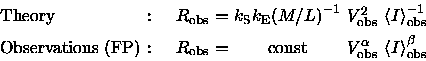 |
(2.17) |
where we have collected the three structural parameters in
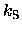 as
as
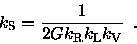 |
(2.18) |
Since the observations give
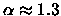 and
and
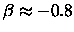 ,
it follows from Eq. (
,
it follows from Eq. (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) )
that
)
that
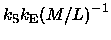 can not be constant,
but has to be the following power law function of
can not be constant,
but has to be the following power law function of
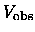 and
and
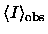
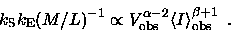 |
(2.19) |
In other words,
either
the structure
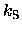 (and
(and
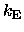 )
or
the mass-to-light ratio
)
or
the mass-to-light ratio
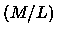 (or both)
need to vary in a systematic way
to produce the observed FP slope.
To explore the possibility of an
(or both)
need to vary in a systematic way
to produce the observed FP slope.
To explore the possibility of an
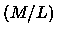 variation further,
we first find an expression for
variation further,
we first find an expression for
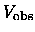 as function of L
from the first line of Eq. (
as function of L
from the first line of Eq. (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) ) and Eq. (
) and Eq. (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) )
)
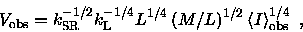 |
(2.20) |
where we have defined
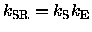 .
We can now eliminate
.
We can now eliminate
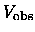 from Eq. (
from Eq. (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) )
and instead get an expression involving L
)
and instead get an expression involving L
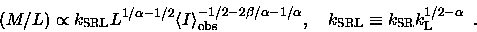 |
(2.21) |
For
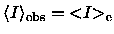 ,
the exponent for
,
the exponent for
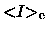 in the above equation
turns out to be non-significantly different from zero.
This is the case for the JFK96 values of
in the above equation
turns out to be non-significantly different from zero.
This is the case for the JFK96 values of 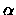 and
and 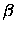 ,
where the
,
where the
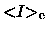 exponent is
exponent is
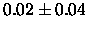 ,
and this is also the case for the FPs studied by e.g. Faber et al. (1987).
Also Prugniel & Simien (1996)
found the
,
and this is also the case for the FPs studied by e.g. Faber et al. (1987).
Also Prugniel & Simien (1996)
found the
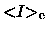 exponent to be non-significant.
Therefore it can be stated,
that the scalar virial theorem (
exponent to be non-significant.
Therefore it can be stated,
that the scalar virial theorem (
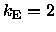 )
and
structural homology (
)
and
structural homology (
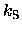 = constant)
implies that the mass-to-light ratio varies with luminosity,
or equivalently with mass, as
= constant)
implies that the mass-to-light ratio varies with luminosity,
or equivalently with mass, as
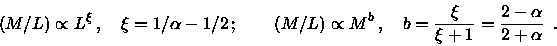 |
(2.22) |
For the value of 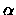 that we find in this study (in Gunn r),
that we find in this study (in Gunn r),
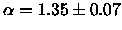 ,
the result is
,
the result is
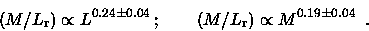 |
(2.23) |
To actually calculate
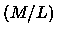 from the data (under the above assumptions),
we need to know the value of
from the data (under the above assumptions),
we need to know the value of
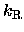 ,
,
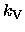 ,
,
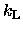 .
For our choice of observables,
.
For our choice of observables,
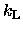 is simply
is simply 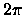 ,
i.e.
,
i.e.
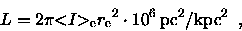 |
(2.24) |
where the identity
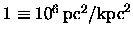 is inserted to denote that we in this study
have
is inserted to denote that we in this study
have
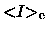 in units of
in units of
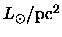 and
and
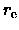 in units of kpc.
in units of kpc.
Modeling is needed to calculate
the constant in the equation for M, Eq. (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) ).
We will here write this equation as
).
We will here write this equation as
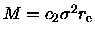 .
Note, that
this dynamical determination of M gives the total mass
.
Note, that
this dynamical determination of M gives the total mass
 ,
which includes luminous matter (stars)
and dark matter.
Bender, Burstein, & Faber (1992)
calculated c2 using models with King profiles
and isotropic velocity dispersions.
Assuming
,
which includes luminous matter (stars)
and dark matter.
Bender, Burstein, & Faber (1992)
calculated c2 using models with King profiles
and isotropic velocity dispersions.
Assuming
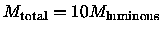 they found
they found
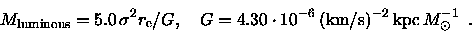 |
(2.25) |
This is for
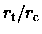 = 100,
with
= 100,
with 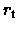 and
and 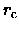 being the tidal and core
radii in the King model, respectively.
For
being the tidal and core
radii in the King model, respectively.
For
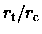 = 300, c2 would be 4.0/G,
since c2 turns out not to be quite constant in their models.
The ratio
= 300, c2 would be 4.0/G,
since c2 turns out not to be quite constant in their models.
The ratio
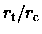 is about 100-300 for giant ellipticals
(Bender et al. 1992).
Equation (
is about 100-300 for giant ellipticals
(Bender et al. 1992).
Equation (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) ) and (
) and (![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) ) combine into
) combine into
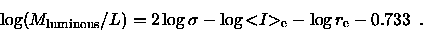 |
(2.26) |
If we want to compare
 for several passbands
with for example prediction from stellar population synthesis models,
the above equation cannot be used for all the passbands.
This is because
for several passbands
with for example prediction from stellar population synthesis models,
the above equation cannot be used for all the passbands.
This is because
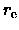 varies with wavelength,
which is also to say that E and S0 galaxies have radial color gradients.
The Bender et al. model does not take this into account.
Instead,
varies with wavelength,
which is also to say that E and S0 galaxies have radial color gradients.
The Bender et al. model does not take this into account.
Instead,
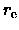 in a common passband ``X'' should be used to calculate the mass,
and
in a common passband ``X'' should be used to calculate the mass,
and
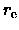 in the given passband ``Y'' to calculate the luminosity, i.e.
in the given passband ``Y'' to calculate the luminosity, i.e.
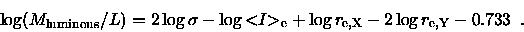 |
(2.27) |
Both equations are independent of the Hubble constant H0,
but since both M and L depend on
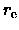 in kpc, which depends on the
distance (cf. Eq.
in kpc, which depends on the
distance (cf. Eq. ![[*]](http://www.astro.ku.dk/Icons/latex2html-96.1/cross_ref_motif.gif) ),
which depends on H0 if the distance is calculated from the redshift,
),
which depends on H0 if the distance is calculated from the redshift,
 becomes proportional to
becomes proportional to  .
.




Next: 2.2.4 Variation of with
Up: 2.2 The Fundamental Plane
Previous: 2.2.2 Is the FP
Properties of E and S0 Galaxies in the Clusters HydraI and Coma
Master's Thesis, University of Copenhagen, July 1997

Bo Milvang-Jensen (milvang@astro.ku.dk)
![]() ).
We will here write this equation as
).
We will here write this equation as
![]() .
Note, that
this dynamical determination of M gives the total mass
.
Note, that
this dynamical determination of M gives the total mass
![]() ,
which includes luminous matter (stars)
and dark matter.
Bender, Burstein, & Faber (1992)
calculated c2 using models with King profiles
and isotropic velocity dispersions.
Assuming
,
which includes luminous matter (stars)
and dark matter.
Bender, Burstein, & Faber (1992)
calculated c2 using models with King profiles
and isotropic velocity dispersions.
Assuming
![]() they found
they found
![]()