We want to be able to calculate the trajectory of a freely falling object (massive or mass less). In special relativity, and in a local intertial frame, a freely falling object moves in a straight line / has a constant velocity. From there, we can go to general coodinates by using the ``trick'' of changing from an ordinary derivative to a covariant derivative. This gives the following equation of motion (also known as the geodesics equation):
, the affine parameter, is a parameter along the curve,
which is unique up to a transformation of the form
(Misner, Thorne, & Wheeler 1973).
A light ray, which I want to study for this project,
moves with the speed of light, which is the same as it has a null
separation, i.e.
.
If we have a metric like the Kerr one and solve for 
we get a 2nd order equation:
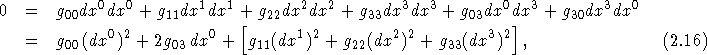
where we have used the symmetry of the metric tensor, i.e.
.
This equation can be readily solved.
Notationwise, we could just as well have used 
instead of 
.
