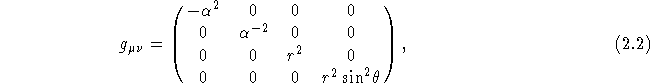
The Schwarzschild metric describes space-time around a spherical mass M which does not have any angular momentum J. The Schwarzschild metric is:
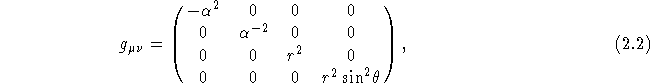
where the lapse function / gravitational redshift factor is:
The more general Kerr metric describes space-time around a spherical mass M which does have an angular momentum J, such as a rotating black hole. The Kerr metric is:
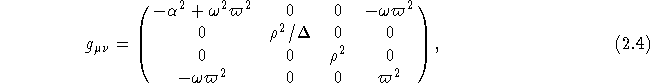
where the Boyer-Lindquist coordinates are:
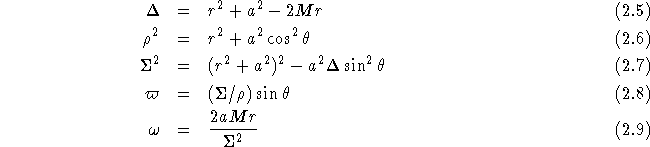
and where the rotation parameter a is defined by
One has 
; an object with higher angular momentum than
corresponding to a = M cannot stick together.
The horizon is the surface which one when using the coordinates of a distant observer in flat space will never see anything pass. It is not a real singularity, but merely a coordinate singularity. It is given by
Another interesting surface is that given by the static limit
, within which is is compulsory to move along the direction of
rotation, since space-time is rotating with so high speed, that even when one
is moving with the speed of light in the opposite direction, one will still
be moving in the direction of rotation.
is given by
The area within the static limit but outside the horizon is called the ergosphere.
Note, that we in all of the above have used ``natural units'',
viz. c = G = 1.
It might, however, be useful to know what absolute sizes I will be talking
about when I say that r is 2, or M is 1.
This can be derived by writing the equation for 
with c and G
included:
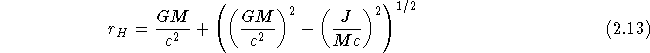
(Berry 1976). We see that length over mass is
