


Next: CROSSING THE FACE
Up: OBSERVATION OF MICROLENSING
Previous: MACHOs
The astrometric effect of
microlensing should be considered
simultaneously with the photometric effect of the same microlensing
event. This was pointed out in a paper
by hoeg.novi, hereafter called HNP.
Three photometric observations were shown to be
in principle sufficient to
determine three parameters of a ``fly-by'' event: The moment
of closest encounter between the dark body and the line of sight to the
star; the characteristic duration, 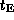 , of the event;
and the impact parameter, i.e., the ratio of the distance to the line
of sight and the Einstein radius.
When these three parameters are known it is in principle sufficient
to obtain three one-dimensional astrometric observations of
the same event in order to derive the proper motion, the distance and
the mass, m, of the dark body. This assumes that the proper motion and the
distance of the background star are accurately known, as can indeed
be assumed. --- For the sake of redundancy and
a better signal-to-noise ratio
it is of course useful to have a much larger number of observations
than just three photometric and three astrometric.
, of the event;
and the impact parameter, i.e., the ratio of the distance to the line
of sight and the Einstein radius.
When these three parameters are known it is in principle sufficient
to obtain three one-dimensional astrometric observations of
the same event in order to derive the proper motion, the distance and
the mass, m, of the dark body. This assumes that the proper motion and the
distance of the background star are accurately known, as can indeed
be assumed. --- For the sake of redundancy and
a better signal-to-noise ratio
it is of course useful to have a much larger number of observations
than just three photometric and three astrometric.
HNP predicts the size of the photometric and
astrometric effects for the ROEMER satellite
project proposed by
lindegren.roemer and hoeg.lindegren.
The photometric effect is more easily detected than the astrometric.
HNP expects more than 300 light amplifications with a
signal-to-noise ratio of at least 10 during a 5 year ROEMER mission.
This expected number of significant amplifications
depends on the total mass of the Galactic
halo of dark bodies,
but not on the distribution function of the masses of the individual
dark bodies. If they all have masses of, e.g.,
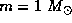 these
amplified photometric observations would belong to about 25 fly-by
events. The dark body masses are,
however, at present assumed to be about 0.1
these
amplified photometric observations would belong to about 25 fly-by
events. The dark body masses are,
however, at present assumed to be about 0.1 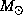 which would
mean that the 300 amplifications would be distributed on a larger
number of events.
The background stars are typically 16th magnitude at distances of 6 kpc.
With GAIA, as described by LP,
the number of such amplifications will be at least an order of
magnitude larger.
Such photometric observations would be
related to MACHOs much closer to the
sun than MACHO observations so far and can therefore provide information
on the local space density of MACHOs, and of the density
in all directions from the sun.
which would
mean that the 300 amplifications would be distributed on a larger
number of events.
The background stars are typically 16th magnitude at distances of 6 kpc.
With GAIA, as described by LP,
the number of such amplifications will be at least an order of
magnitude larger.
Such photometric observations would be
related to MACHOs much closer to the
sun than MACHO observations so far and can therefore provide information
on the local space density of MACHOs, and of the density
in all directions from the sun.
The expected time scales of events are given in HNP-Table 1;
e.g., for stars of V= 16 mag we get 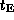 = 8 or 25 days if all halo dark
bodies have the mass m= 0.1 or 1.0
= 8 or 25 days if all halo dark
bodies have the mass m= 0.1 or 1.0 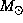 , respectively.
, respectively.
The detection of microlensing from a scanning astrometric satellite
is characterized by an uneven distribution in time of the
observations, due to the strict scanning law. This is very different
from the rather uniform distribution of ground based MACHO
observations. A discussion of this subject is given in HNP, but it can
be said that the uneven distribution offers advantages and
disadvantages; many possible time scales will be sampled, but the
sampling will be incomplete.
The astrometric measurements with ROEMER and GAIA are one-dimensional,
as assumed above.
HNP shows that a satellite giving astrometric observational errors
20 times smaller than ROEMER -- and those of GAIA will be even smaller
than that --
would give a significant determination of the proper motion of a MACHO
of 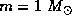 passing close to a 16th magnitude star.
Proper motion and distance give the tangential velocity, and thus a
clue to the space velocity, otherwise inferred only from models of the
halo.
passing close to a 16th magnitude star.
Proper motion and distance give the tangential velocity, and thus a
clue to the space velocity, otherwise inferred only from models of the
halo.
HNP considered the prospects for astrometric observations of MACHOs to
be meagre. But the paper was written in May 1994, and since then
the prospects for
space astrometry have improved drastically through
new technical ideas and owing to
initiatives by the European Space Agency.



Next: CROSSING THE FACE
Up: OBSERVATION OF MICROLENSING
Previous: MACHOs
Erik Hg
Tue Aug 8 06:38:24 MET DST 1995
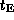 , of the event;
and the impact parameter, i.e., the ratio of the distance to the line
of sight and the Einstein radius.
When these three parameters are known it is in principle sufficient
to obtain three one-dimensional astrometric observations of
the same event in order to derive the proper motion, the distance and
the mass, m, of the dark body. This assumes that the proper motion and the
distance of the background star are accurately known, as can indeed
be assumed. --- For the sake of redundancy and
a better signal-to-noise ratio
it is of course useful to have a much larger number of observations
than just three photometric and three astrometric.
, of the event;
and the impact parameter, i.e., the ratio of the distance to the line
of sight and the Einstein radius.
When these three parameters are known it is in principle sufficient
to obtain three one-dimensional astrometric observations of
the same event in order to derive the proper motion, the distance and
the mass, m, of the dark body. This assumes that the proper motion and the
distance of the background star are accurately known, as can indeed
be assumed. --- For the sake of redundancy and
a better signal-to-noise ratio
it is of course useful to have a much larger number of observations
than just three photometric and three astrometric.



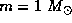 these
amplified photometric observations would belong to about 25 fly-by
events. The dark body masses are,
however, at present assumed to be about 0.1
these
amplified photometric observations would belong to about 25 fly-by
events. The dark body masses are,
however, at present assumed to be about 0.1 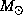 which would
mean that the 300 amplifications would be distributed on a larger
number of events.
The background stars are typically 16th magnitude at distances of 6 kpc.
With GAIA, as described by LP,
the number of such amplifications will be at least an order of
magnitude larger.
Such photometric observations would be
related to MACHOs much closer to the
sun than MACHO observations so far and can therefore provide information
on the local space density of MACHOs, and of the density
in all directions from the sun.
which would
mean that the 300 amplifications would be distributed on a larger
number of events.
The background stars are typically 16th magnitude at distances of 6 kpc.
With GAIA, as described by LP,
the number of such amplifications will be at least an order of
magnitude larger.
Such photometric observations would be
related to MACHOs much closer to the
sun than MACHO observations so far and can therefore provide information
on the local space density of MACHOs, and of the density
in all directions from the sun.
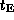 = 8 or 25 days if all halo dark
bodies have the mass m= 0.1 or 1.0
= 8 or 25 days if all halo dark
bodies have the mass m= 0.1 or 1.0 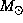 , respectively.
, respectively.
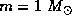 passing close to a 16th magnitude star.
Proper motion and distance give the tangential velocity, and thus a
clue to the space velocity, otherwise inferred only from models of the
halo.
passing close to a 16th magnitude star.
Proper motion and distance give the tangential velocity, and thus a
clue to the space velocity, otherwise inferred only from models of the
halo.